Electromagnetic Induction

Purpose:  In this lab, we go into greater deteal on how electromagnetic inductance works. We, then, start to go into inductors and their applications.

Induced EMF

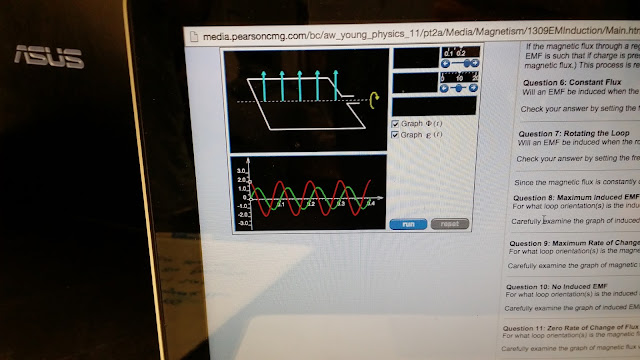
We begin to look at how the voltage behaves when the magnetic flux changes. We do this by examining an online program that graphs the behavior of the voltage or the emf as the magnetic flux changes. The website, also, has some questions that we would later answer. We can see that there is a correlation between that magnetic flux and the emf by the graph shown.

We answer the questions that the website had supplied. Overall, we conclude that there is a reaction when the magnetic flux changes. This reaction causes an induced emf which counteracts that change in the magnetic flux. We found that the change in the flux could be by the change in the magnitude of the magnetic field that passes through a loop, a change in the area of the loop, and the change in the orientation of the loop. We found that the induced emf is greatest the moment that there is no flux and that the magnetic flux changes most rapidly when the area of the loop is large. We see that the instantaneous change in the magnetic flux is zero when the area vector is parallel to the magnetic field vector (or the magnetic field is going the the largest possible area of the loop). When we examine this instant, we see that there is no induced emf. Therefore, we conclude that the induced emf is proportional to the change in the magnetic flux. Also, when observing the graph, we see that the induced emf the negative value of the change in the flux (if flux has a positive slope, induced emf is negative).

Movable Rod Acting As A Wire

Professor Mason sets up a circuit in which a rod acts as a wire that connected the two metal rails. We can also see that there is a magnet set up within the circuit. One of the rails are connected to a power supply and the other rail is grounded. 

We are able to see that the rod moves as there is a force acting on the rod. This is because there is current through the rod and this current is going through a magnetic field. This interaction causes a force on the rod that is perpendicular to the current and the magnetic field. The way the current flows dictates with direction the rod moves. We also see that the rod moving causes a change in the magnetic flux.

We proceed to expand on the experiment that Professor Mason had demonstrated and the ideas of the change in magnetic flux.

We find that as the bar moves at a constant velocity due to the magnetic force, there is a change in the magnetic flux. We found out, earlier, that the change in magnetic flux induces an emf. Our job was to find out how to find the induced emf. We were able to do this by examining the way the area changes. We know that the length of the rod never changes but the position of it does. We were able to see that we can write its displacement in terms of its velocity and the time the rod takes to travel the displacement. Multiplying this to the length of the rod gives us the change in the area in terms of the velocity, the time, and the length of the rod. We would later incorporate this with the definition of the magnetic flux, which is the magnetic field times the area. Since the area is changing, we get the change in the flux, which gives us the induced emf. In this case, the induced emf is positive as the area of the loop decreases because the rate at which the flux changes is negative, and we previously discussed that the induced emf has to be opposite of the change in flux. The induced current, then, tried to counteract the change in the magnetic flux with its own magnetic field. We know that a current generates a magnetic field in a cyclone fashion around the current. The direction of the magnetic field of the current is what counteracts the change in the flux. If flux decreases, the current flows in a way that generates a magnetic field to increase the flux.

Beginning Of Inductors

We do some derivations on the left side of our board involving inductors. We start off by writing the length of the inductor is equal to the negative potential across the inductor divided by the rate of the current. We, also, used the relationships between capacitance and charge to formulate the voltage across a capacitor as the current changes. As the current changes, the voltage does as well. In the middle, we work out a problem to find the inductance using the given physical parameters of the inductor. The inductance is found by the red formula by the number of loops, that area of the of the loop, the permeability, and the length of the inductor. We, also, derive the units of the inductance in the right side of the board.

On our white board, we discuss how inductors work. Inductors, generally, resist rapid changes in voltage.

We answer some final questions involving inductors and how they effect circuits.

We find that when we have an inductor in a circuit and run a current through it, there is an induced emf the opposes the emf of the battery. This is because the current generates a change in the magnetic flux through the loops and since there is a change in flux, there is a negative emf. The current vs. time graph shows us that the current increases to some maximum value and this is because the change in flux approaches zero as time goes by. This means that the current then becomes reliant on the power supply and the resistor in the circuit. We, then, find that the time for the current to hit equilibrium is dependent on the inductor as well as the resistor. Time increases and the inductor increases and decreases as the resistor increases. This is because if we have a larger inductor, a larger emf is produced and this causes the current to take longer to reach equilibrium. However, if we increase the resistance, we decrease the equilibrium value of the current which means the time to get to equilibrium is faster.

Conclusion:  We found that the induced emf was dependent on the negative change in the magnetic flux. We can change the flux by changing the area of the loop, orientation of the loop, and magnitude of the magnetic field. We, also, looked at how the flux changes in the experiment done by Professor Mason. We concluded that there is an induced current that generates a magnetic field to counteract the change in the magnetic flux. The direction of the magnetic field going through the loop and well as the way the area of the loop changes dictates which way the current flows. Finally, we took a look at inductors and the way they impact circuits. Inductors generate changes in magnetic flux which generates an induced emf. This causes the current start of at zero and reach equilibrium with time. This time was also found to be dependent on the resistor and the inductor.