Electric Potential

Purpose:  We, further, go into the concept of electric potential by going over some examples that are different than just two point charges. We, also, go into some hands-on activities for electric potential.

Potential Of A Charged Ring

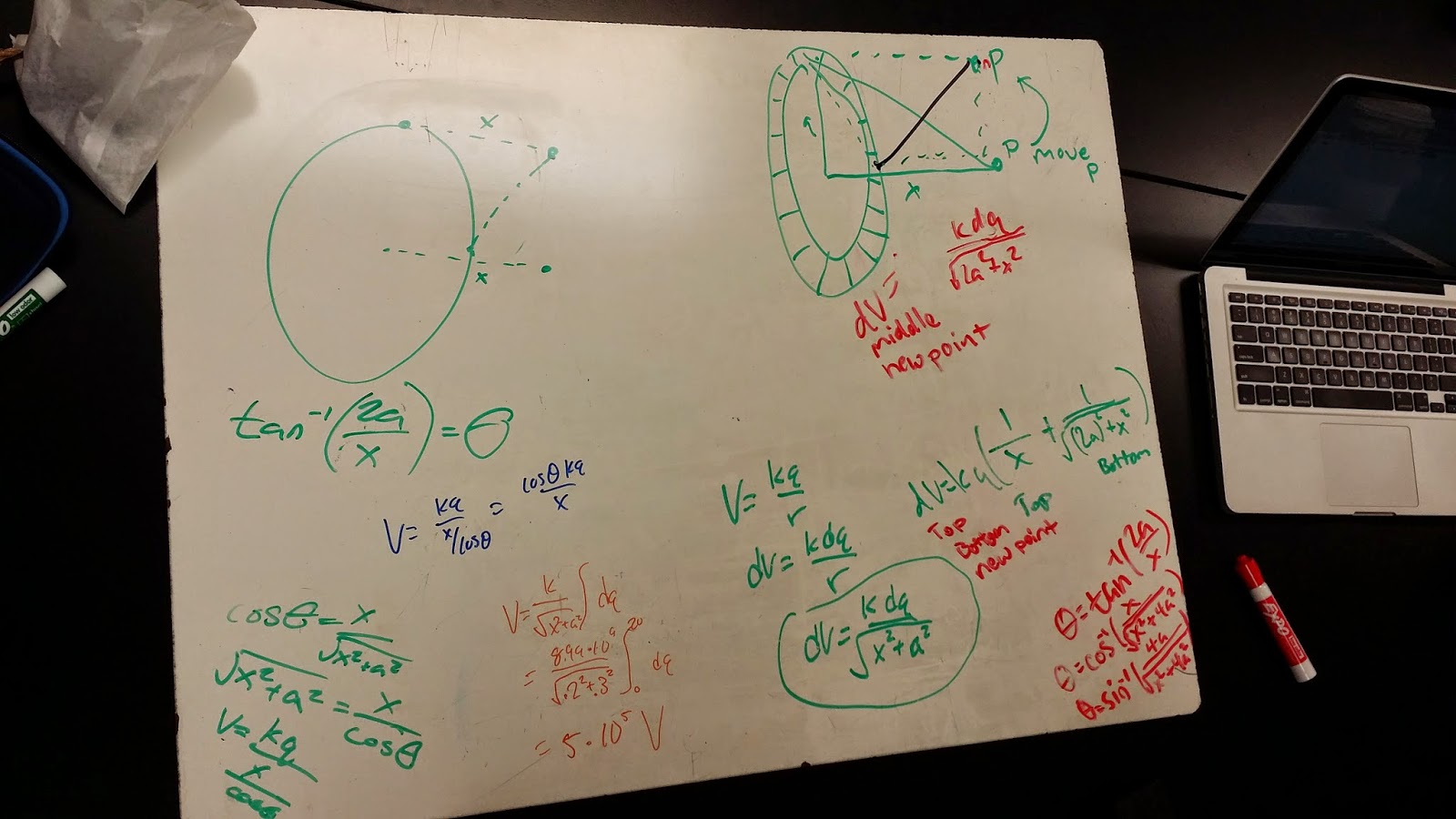
To begin our first potential problem, he had a ring with some charge on it. We then knew the variable dimensions of the ring and the potential point we are trying to find. The first point is in the center of the ring at some x distance away. We, then, start with the standard equation for potential, but this only applies to point charges. We alter the equation by saying the change in our potential is proportional to the change in q. After, we integrate to find the potential.

Potential Of A Charged Ring At A Different Location

Next, we use the same ring to find the potential at a different location. The twist here is that the location is positioned where it is difficult to take advantage of symmetry because the point is positioned at the top corner of the ring at some distance away. The key here is getting the proper distance that the point is from the ring. Using geometric representations, we are able to find that it is an x distance away from the ring and if a is the radius of the ring, we can say that the potential changes as the a distance increase and decreases.It increases and decreases because as we are taking infinitesimally small segments of dq, we integrate around the ring. This changes the a value. We can express this in terms of the change in the angle and solve for the potential.

Finding Potential Using E-Field

We work with the first problem of a charged ring and find the potential at a point x away from the ring centered in the middle of the ring. This time, we solve for the electric field the charged ring produces and use the definition for potential to solve for the potential of the ring at that distance. By definition, the potential difference is equal to the negative integral of the dot product of the electric field and the distance from infinity to the distance. When we solve for the potential this way, we get the same conclusion we saw before.

Using Excel To Find Potential

We continue with a different problem that is similar to the ring. This time, we have a wire of the length and solve for its potential and distance above the wire at the center of the wire using an excel spreadsheet. We decided to break the ring into 20 segments. We, then, solve for the potential at a segment using the center of the segment as the point charge. Once we have the potential of one segment, we multiply by the number of segments. This gives us nearly the same numerical value for potential of the ring.

We continue to solve for the same wire problem but we approach it differently. Instead, we look at the change in the radial distance and the potential it has throughout this change. This is very similar to the integral method. Once we have the potentials at every distance, we add up all of the potentials and in the end, we and up with the same answer we received from the previous excel sheet.

Potential By Integration

We can find the potential of a wire at any distance above it using the integral method. We determine the the y component does not change but the x does. We the write of an equation for the potential that expresses the change in the x direction. If we know where the point we are looking for is positioned with respect to the wire, we can easily solve for the potential using integration with the correct integration bounds.

Finding Potentials Along A Dipole

We start a hands-on experiment for finding the potential. We use a piece of conducting paper and this paper is nailed down to some insulating material. The nails are given an opposite charge and this creates a dipole along the conductive paper. Using the red and black pins, we are able to measure the potential at any point with respect to one of the charges.

This is how we set up the experiment. We hooked up our nails to some power supply. We, then used the multimeter to measure the potential at any point on the conductive paper.

This image includes a summary of our findings for the experiment. After finding the potentials along the x-axis, we were able to find the potential difference as well as the work required to move a charge from one location to the other. Finding the work just requires us to find the potential difference and then multiplying by the value of the charge we are trying to move. This is consistent, as energy is equal to the potential times the charge.

We found that as the radial distance approaches zero, we get infinite potential and as the radial distance approaches infinity, we get zero potential.

Conclusion:  We experimented with various ways to find potential from a distribution of charge. These methods include excel arithmetic and integration. Depending on the charged figure, it may be easier to use an excel sheet to find potential. We, also, received a hands-on view of potential when we determined the potential at various points of a dipole. We conclude that potential is zero infinitely far away and infinite at the source.